定长定角构造辅助圆问题
问题描述
在矩形ABC中,AB等于2√2,AD等于4。P是矩形内的一个动点,且始终保持着∠APB=90度。求DDP的最小值。
解题思路
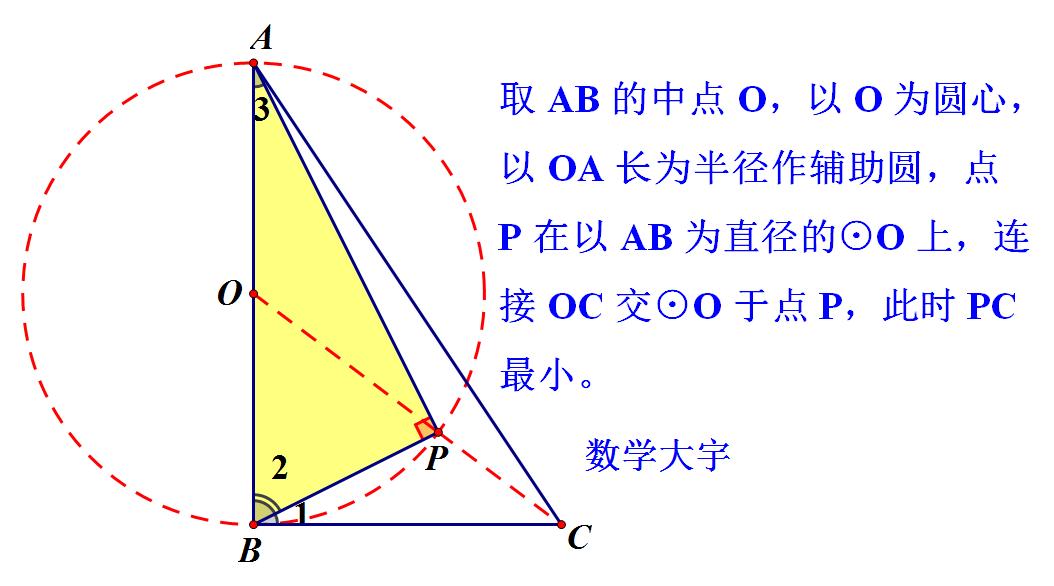
要求解DP的最小值,需要探究P的运动轨迹,而P的运动轨迹是一个关键点。根据题意,我们可以发现矩形ABC中的AB是一个直径,所以可以以AB的中点为圆心构造一个辅助圆。P点在这个圆上运动。
最小值分析
要求解DP的最小值,在圆中是圆外一点和圆上一点的最小值,即过圆心和圆上一点的线段最短。我们可以通过分析不共线情况下的三角形来解释这点。若不共线,则组成一个三角形,在这个三角形中,任意两边之和大于第三边,所以DP永远大于OD。而当OPD三点共线时,DP和OP的和等于OD,即DP最短。所以最小值出现在当OPD三点共线的情况下,此时OP的最小值等于OD减去OP。
计算最小值
OD在三角形AOD中是斜边,所以OD等于√(OA²+AD²),即√(2²+4²)=√18。半径OP等于√2。所以最小值为√18-√2=2√2。
小结
通过本题,我们可以得出以下两个需要注意的问题: 1. 定长定角线圆形的问题:要找到直径所对应的圆周角为90度,构造一个辅助圆。 2. 最小值问题:通过穿心线的概念,即过圆心和圆上一点的线段最短,可以求得DP的最小值。
通过以上分析和计算,可以得出最终答案为2√2。