在学习几何的过程中,掌握八个角对内分割和对外补形是非常重要的。这些概念可以帮助我们更好地理解几何问题,并解决一些简单的图形问题。
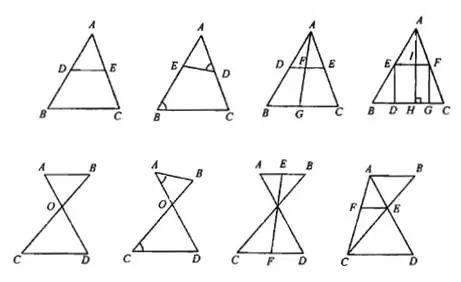
例如,我们看到一个等腰直角三角形,其中角ABC等于90度、AB和BC相等,D是BC边上的中点。问题是求AF比上FC的值。直接求解可能稍有困难,但如果我们将图形补成正方形,就可以大大增加信息量。我们再过B点做A的一个垂线延长到AC上,形成一个阿尔法角和一个贝塔角相等的等腰直角三角形,然后利用全等关系就可以得出AF比上FC的比值。通过补正方形,我们成功地解决了这个问题。细心的读者可能已经发现,以上转写自口播语音的文章缺乏分段和层次分明的结构,不利于阅读理解。下面我们将对此进行改进,使文章更符合书面文字的规范。在学习几何的过程中,掌握八个角对内分割和对外补形是非常重要的。这些概念可以帮助我们更好地理解几何问题,并解决一些简单的图形问题。
例如,我们看到一个等腰直角三角形,其中角ABC等于90度、AB和BC相等,D是BC边上的中点。问题是求AF比上FC的值。直接求解可能稍有困难,但如果我们将图形补成正方形,就可以大大增加信息量。我们再过B点做A的一个垂线延长到AC上,形成一个阿尔法角和一个贝塔角相等的等腰直角三角形,然后利用全等关系就可以得出AF比上FC的比值。通过补正方形,我们成功地解决了这个问题。
