汪保鸿
题目分析：
这篇文章介绍了如何解决一个几何题。作者强调了一些关键概念，如垂直、半角、全等等，并展示了如何应用这些概念来解题。
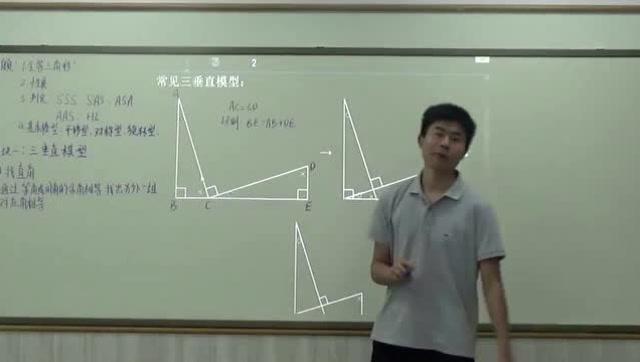
三垂直和半角的重要性：
作者首先提到，即使在阅读题目之前，根据图形的特点也能确定要用到哪些知识点，例如三垂直和半角概念。这是解题的第一步。
解题步骤：
三垂直： 作者强调了三垂直概念，即垂直的三边形成的角相等，这可以用于推导一些边的长度。
半角模型： 作者提到半角模型，其中一个边与其他两边之和的关系可以用于计算半角。作者指出如果一边与4相等，另一边与6相等，那么半角就是2。
全等三角形： 根据三垂直原理，可以得出两个全等的三角形，从而确定一些边的长度。
确定边长： 作者建议将正方形的边长设为X，然后利用已知的关系，如X+6，来得到X的值。
应用知识解题：
作者强调了解题的关键是将已知的关系写下来，然后应用这些关系来解决问题。通过逐步解析图形并确定边长X，作者最终解决了问题，找出PK的长度。
总结：
这篇文章教授了如何在解几何题时应用重要的几何概念，如垂直、半角和全等。作者通过逻辑推理和关系建立，演示了如何解决这一特定几何问题。
数学老师董小磊
2023-10-17 09:38:53
令狐瑞瑗
寿桂明
莘苑弘
终宜宏
管韦玲
劳逸惠
黄羽静
阙谦海
都娴梵
柏贤岩
吉星进
司空才心